All the Graphs You Need to Know for Microeconomics

Three types of graphs are used in this course: line graphs, pie graphs, and bar graphs. Each is discussed beneath.
Line Graphs
The graphs nosotros've discussed then far are called line graphs, considering they evidence a human relationship between two variables: one measured on the horizontal axis and the other measured on the vertical axis.
Sometimes it's useful to bear witness more than one set of data on the same axes. The data in the table, below, is displayed in Effigy 1, which shows the relationship between two variables: length and median weight for American baby boys and girls during the commencement 3 years of life. (Themedian means that half of all babies counterbalance more than this and half weigh less.) The line graph measures length in inches on the horizontal centrality and weight in pounds on the vertical axis. For case, point A on the figure shows that a male child who is 28 inches long will have a median weight of nigh 19 pounds. One line on the graph shows the length-weight relationship for boys, and the other line shows the relationship for girls. This kind of graph is widely used by wellness-care providers to check whether a kid'south physical development is roughly on track.

Figure 1. The Length-Weight Relationship for American Boys and Girls
| Boys from Birth to 36 Months | Girls from Nativity to 36 Months | ||
|---|---|---|---|
| Length (inches) | Weight (pounds) | Length (inches) | Weight (pounds) |
| twenty.0 | eight.0 | 20.0 | 7.ix |
| 22.0 | 10.5 | 22.0 | 10.5 |
| 24.0 | 13.5 | 24.0 | 13.ii |
| 26.0 | 16.iv | 26.0 | xvi.0 |
| 28.0 | xix.0 | 28.0 | 18.8 |
| 30.0 | 21.8 | 30.0 | 21.2 |
| 32.0 | 24.3 | 32.0 | 24.0 |
| 34.0 | 27.0 | 34.0 | 26.ii |
| 36.0 | 29.3 | 36.0 | 28.9 |
| 38.0 | 32.0 | 38.0 | 31.three |
Not all relationships in economics are linear. Sometimes they are curves. Figure 2, below, presents another example of a line graph, representing the data from the tabular array underneath. In this case, the line graph shows how sparse the air becomes when you climb a mountain. The horizontal axis of the figure shows distance, measured in meters above sea level. The vertical axis measures the density of the air at each altitude. Air density is measured past the weight of the air in a cubic meter of space (that is, a box measuring one meter in peak, width, and depth). As the graph shows, air pressure is heaviest at basis level and becomes lighter every bit you climb. Figure 1 shows that a cubic meter of air at an altitude of 500 meters weighs approximately one kilogram (near 2.2 pounds). However, every bit the altitude increases, air density decreases. A cubic meter of air at the top of Mount Everest, at almost 8,828 meters, would weigh only 0.023 kilograms. The thin air at high altitudes explains why many mountain climbers demand to utilize oxygen tanks as they reach the top of a mountain.
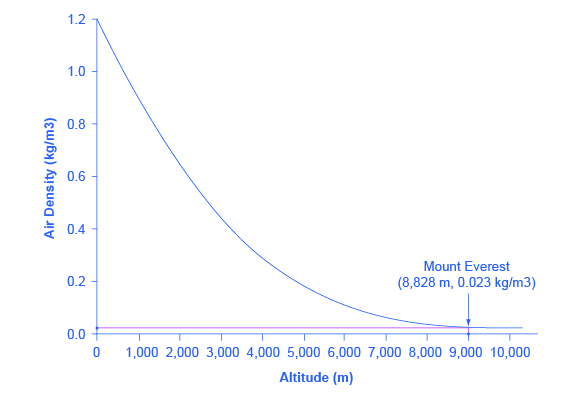
Figure 2. Distance–Air-Density Human relationship
| Distance (meters) | Air Density (kg/cubic meters) |
|---|---|
| 0 | ane.200 |
| 500 | 1.093 |
| i,000 | 0.831 |
| 1,500 | 0.678 |
| 2,000 | 0.569 |
| 2,500 | 0.484 |
| three,000 | 0.415 |
| three,500 | 0.357 |
| iv,000 | 0.307 |
| 4,500 | 0.231 |
| 5,000 | 0.182 |
| 5,500 | 0.142 |
| half-dozen,000 | 0.100 |
| 6,500 | 0.085 |
| 7,000 | 0.066 |
| 7,500 | 0.051 |
| 8,000 | 0.041 |
| eight,500 | 0.025 |
| 9,000 | 0.022 |
| 9,500 | 0.019 |
| 10,000 | 0.014 |
The length-weight relationship and the altitude–air-density human relationship in these two figures represent averages. If you were to collect actual data on air pressure at different altitudes, the same altitude in different geographic locations would take slightly different air density, depending on factors similar how far yous were from the equator, local weather conditions, and the humidity in the air. Similarly, in measuring the height and weight of children for the previous line graph, children of a particular top would have a range of different weights, some in a higher place average and some beneath. In the real earth, this sort of variation in data is common. The chore of a researcher is to organize that data in a mode that helps to understand typical patterns. The study of statistics, particularly when combined with computer statistics and spreadsheet programs, is a smashing help in organizing this kind of information, plotting line graphs, and looking for typical underlying relationships. For most economics and social science majors, a statistics course volition exist required at some indicate.
Ane common line graph is called a time series, in which the horizontal centrality shows fourth dimension and the vertical axis displays some other variable. Thus, a time-serial graph shows how a variable changes over fourth dimension. Effigy 3 shows the unemployment charge per unit in the U.s.a. since 1975, where unemployment is defined as the percentage of adults who want jobs and are looking for a job, but cannot find one. The points for the unemployment charge per unit in each twelvemonth are plotted on the graph, and a line so connects the points, showing how the unemployment charge per unit has moved up and down since 1975. With a graph like this, information technology is easy to spot the times of high unemployment and of low unemployment.
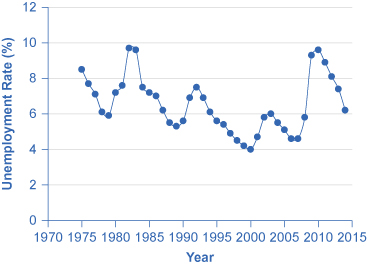
Figure three. U.Due south. Unemployment Rate, 1975–2014
Pie Graphs
A pie graph (sometimes called a pie chart) is used to show how an overall total is divided into parts. A circumvolve represents a group equally a whole. The slices of this circular "pie" show the relative sizes of subgroups.
Effigy 4 shows how the U.S. population was divided among children, working-historic period adults, and the elderly in 1970, 2000, and what is projected for 2030. The information is starting time conveyed with numbers in the table, below, and then in 3 pie charts.
| Twelvemonth | Total Population | 19 and Under | xx–64 years | Over 65 |
|---|---|---|---|---|
| 1970 | 205.0 1000000 | 77.2 (37.6%) | 107.7 (52.5%) | twenty.i (9.8%) |
| 2000 | 275.4 million | 78.4 (28.five%) | 162.two (58.9%) | 34.eight (12.6%) |
| 2030 | 351.ane meg | 92.6 (26.4%) | 188.2 (53.6%) | 70.3 (20.0%) |

Figure 4. Pie Graphs of the U.S. Age Distribution (numbers in millions)
In a pie graph, each piece of the pie represents a share of the full, or a percentage. For example, fifty% would be one-half of the pie and twenty% would be one-5th of the pie. The three pie graphs in Effigy iv show that the share of the U.S. population 65 and over is growing. The pie graphs permit you to get a feel for the relative size of the different age groups from 1970 to 2000 to 2030, without requiring yous to slog through the specific numbers and percentages in the table. Some common examples of how pie graphs are used include dividing the population into groups past age, income level, ethnicity, religion, occupation; dividing different firms into categories past size, industry, number of employees; and dividing up government spending or taxes into its main categories.
Bar Graphs
A bar graph uses the tiptop of unlike bars to compare quantities. The table, below, lists the 12 most populous countries in the world. Figure v provides this same information in a bar graph. The height of the confined corresponds to the population of each country. Although you may know that Red china and Republic of india are the virtually populous countries in the earth, seeing how the bars on the graph tower over the other countries helps illustrate the magnitude of the difference betwixt the sizes of national populations.

Figure 5. Leading Countries of the World by Population, 2015 (in millions)
| Country | Population |
|---|---|
| Prc | 1,369 |
| India | 1,270 |
| Usa | 321 |
| Republic of indonesia | 255 |
| Brazil | 204 |
| Islamic republic of pakistan | 190 |
| Nigeria | 184 |
| Bangladesh | 158 |
| Russia | 146 |
| Japan | 127 |
| Mexico | 121 |
| Philippines | 101 |
Bar graphs tin can be subdivided in a style that reveals information similar to that nosotros tin become from pie charts. Effigy six offers three bar graphs based on the information from Figure 4 about the U.South. age distribution in 1970, 2000, and 2030. Figure 6 (a) shows three bars for each year, representing the full number of persons in each age subclass for each yr. Figure vi (b) shows only one bar for each yr, but the unlike age groups are now shaded inside the bar. In Figure 6 (c), nonetheless based on the same data, the vertical centrality measures percentages rather than the number of persons. In this case, all three bar graphs are the same peak, representing 100 percent of the population, with each bar divided according to the per centum of population in each age group. It is sometimes easier for a reader to run his or her eyes beyond several bar graphs, comparing the shaded areas, rather than trying to compare several pie graphs.

Figure half-dozen. U.S. Population with Bar Graphs
Figure v and Figure half dozen show how the bars tin represent countries or years, and how the vertical axis tin can represent a numerical or a percentage value. Bar graphs tin can also compare size, quantity, rates, distances, and other quantitative categories.
Comparing Line Graphs, Pie Charts, and Bar Graphs
At present that you are familiar with pie graphs, bar graphs, and line graphs, how do you know which graph to use for your data? Pie graphs are oftentimes meliorate than line graphs at showing how an overall group is divided. Nevertheless, if a pie graph has too many slices, information technology can get difficult to interpret.
Bar graphs are peculiarly useful when comparing quantities. For example, if you are studying the populations of unlike countries, as in Figure v, bar graphs tin show the relationships between the population sizes of multiple countries. Not only can it prove these relationships, but it tin as well evidence breakdowns of dissimilar groups within the population.
A line graph is oft the most constructive format for illustrating a relationship betwixt two variables that are both irresolute. For case, time-serial graphs can show patterns equally time changes, like the unemployment rate over time. Line graphs are widely used in economics to nowadays continuous data about prices, wages, quantities bought and sold, the size of the economy.
Cocky Check: Graphs in Economics
Answer the question(s) beneath to see how well you understand the topics covered in the previous section. This short quiz does notcount toward your grade in the form, and you can retake it an unlimited number of times.
You'll have more success on the Self Cheque if you lot've completed the three Readings in this section.
Apply this quiz to bank check your understanding and make up one's mind whether to (1) study the previous section further or (2) move on to the side by side section.
Source: https://courses.lumenlearning.com/suny-microeconomics/chapter/reading-types-of-graphs/
0 Response to "All the Graphs You Need to Know for Microeconomics"
Post a Comment